This is a tough question and if someone can provide a commonsense answer then they must know what they are talking about. Well here we go!
To be relevant the calculation for an optimum order quantity should take account of 100 years of industrial engineering and operations research.
So ….. below we review the 4 main models used to replicate the behavior of supply chains and therefore define optimum order quantities.
Finally we try to bring it all together and come up with a pragmatic and accessible approach to calculating the optimum order quantity.
The 4 models are;
- Economic Order Quantity (EOQ) model
- Wagner-Whitin model
- Base Stock model
- (Q,r) model
1. EOQ Model
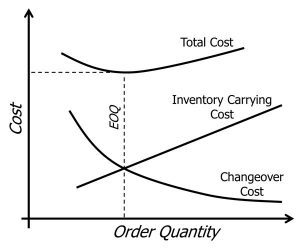
This model first appeared in the operations research literature around 1913 and it seeks to find that order quantity that minimises the combined costs of changeovers and inventory holding as shown in the graphic below.
The equation for the production quantity that results in the lowest total changeover plus inventory cost is;
EOQ = Square Root of ((2 X COC X D)/(V X r))
where COC = changeover cost, D = demand per time period, V = unit cost of the material, r = percent carrying cost of inventory per time period.
Not many people realise that this model relies on some unreal assumptions including;
- Production is Instantaneous (there is no capacity constraint)
- Delivery is Immediate (no time lag between production and availability)
- Demand is Deterministic (no uncertainty about quantity or timing of demand)
- Demand is Constant over Time (represented as a straight line)
- Production incurs a Fixed Set-up (regardless of lot size)
- Products can be Analysed Individually (no interactions between products)
The Secret About EOQ
We thought about dedicating this post to the EOQ model because it has one important and redeeming feature; the sum of the inventory holding and changeover costs is fairly insensitive to increases or decreases in the order quantity.
Stated another way, if we vary the order quantity around the nominal EOQ value then we won’t incur much additional cost. This will weigh heavily on our final conclusion below.
2. Wagner-Whitin Model
The Wagner-Whitin model was developed in 1958 to try and deal with problem 3. above.
Problems 1. and 2. were simply seen as a phasing issue (ie. introduce a lag between when the order was ordered and when it was actually required).
The Wagner-Whitin model adjusted the order quantity dynamically according to forward looking demand. The algorithm created an optimum order which took into account set-up costs and demand over a certain horizon. It still assumed that demand was deterministic but varied.
The problem with the Wagner-Whitin model is that there is no uncertainty in demand or supply (eg. order cancellations, yield loss, schedule deviations, etc). This is essentially the model (and therefore the weaknesses) that was carried over into today’s MRP systems.
If demand is uncertain then there are really only two approaches to take;
- Continue to model demand as if it were deterministic and modify the data to account for uncertainty (a.k.a MRP). Unfortunately supply chains are getting more complex by the year and so this is untenable. The rescheduling load will become more frequent and more complex as demand and supply become more variable.
- Replicate uncertainty in the reordering model using statistical modelling techniques.
As a result of this “fork in the road” two models appeared as the main contenders for dealing with the problem of demand uncertainty using statistical techniques; “The Base Stock Model” and the “(Q,r) Model”.
3. Base Stock Model
Here the inventory is replenished one unit at a time as random demands occur. Demand variation is completely absorbed by the inventory, so that the only issue is to determine the reorder point. The target inventory level we set for the system, and hence the inventory that absorbs demand uncertainty, is known as a base stock level, and hence the name of the model.
There is a lot of literature on this model and understanding the way to calculate the base stock is essential to minimising the risk of stockouts by taking into account backorder costs and inventory holding costs. This model assumes replenishment of one unit at a time with no reference to set-up costs.
This model may work for a fridge manufacturer or a car manufacturer who uses paced assembly lines (targeting “one-piece-flow”) but it is impracticable for flow lines which work off “bulk” order quantities due to the futility of producing single quantities such as say 1 litre. Enter the (Q,r) model.
4. (Q,R) Model
The first formal publication regarding this model was in the Harvard Business Review in 1934. The (Q,r) model addresses two issues simultaneously;
- Establishes the re-order point (r) or safety stock, as in the base stock model, with all the statistical nuance that that incurs
- Establishes how many to order or produce at a time (Q), as a statistically optimised version of EOQ.
The (Q,r) model optimises Q and r for inventory holding costs, order frequency according to a fixed set-up cost valuation, and customer service according to a nominal valuation of backorder/stockout costs.
The replenishment quantity Q affects cycle stock (i.e. inventory held to avoid excessive replenishment costs) and the reorder point affects safety stock (ie. inventory held to avoid stockouts). Note that under these definitions, all the inventory held in the EOQ model is cycle stock, while all the inventory held in the base stock model is safety stock. In this sense, the (Q,r) model represents the synthesis of these two models.
The issue with the (Q,r) model is that it is very complicated and inaccessible for the lay planner. The technical notes relating to this model span 12 pages and incorporate pure maths and statistical analysis. Like all good analysis though it does provide other insights, the biggest being;
- Cycle Stock increases as replenishment frequency decreases.
- Safety Stock provides a buffer against stockouts.
Well we probably knew that from the EOQ model and the Base Stock model, but the (Q,r) model brings it all together in one model.
So where does that leave us in terms of answering the question, What is my optimum order quantity?
Well the answer is that it depends on the unique behaviour of the material being managed and is a combination of our supply strategy for that item (including production capacity), the customers’ tolerance for delays, and the extent to which variability has been mitigated within the supply chain.
We need a way to represent all of this in a more user-friendly model, something that doesn’t throw out the insights from the operations research models (above) but deals with the complexity in a more intuitive and accessible way …….
So ….. What’s the answer??
The EOQ model is a good place to start when designing or optimising a supply chain. The EOQ for each material or product (remembering that this is the order at the company or supplier factory) should be established with data on the changeover costs, average demand and inventory carrying costs.
This will yield an EOQ that can still be adjusted considerably without a big impact on total costs (remembering that the sum of the inventory holding and changeover costs is fairly insensitive to increases or decreases in the order quantity).
The next step is to adjust the order quantity according to whatever load leveling approach you (or your supplier) are using at the factory.
This then is the optimum order quantity for each material HOWEVER we need to set a few things in place to account for all the operations research from the Wagner-Whitin, Base Stock and (Q,r) models as well as accounting for all the weaknesses of the EOQ model;
- supply and demand will vary so, for a make-to-stock inventory position, a buffer stock must be established and maintained. This stock level should be calculated using customer service targets, historical variation data and historical demand data. Make-to-order positions will need a time buffer to shelter the customer from demand and supply variability.
- average demand will trend up or down over time so all quantities must be recalculated (manually or automatically) as changes in the supply chain occur. These changes will include sales growth or decline, product ramp-down and ramp-up, structural changes to the supply chain such as warehouse relocations, etc.
Here are our articles on 2 different approaches to inventory buffer sizing;